角平分線的性質(zhì)角平分線可以得到兩個相等的角，角平分線上的點到角兩邊的距離相等。

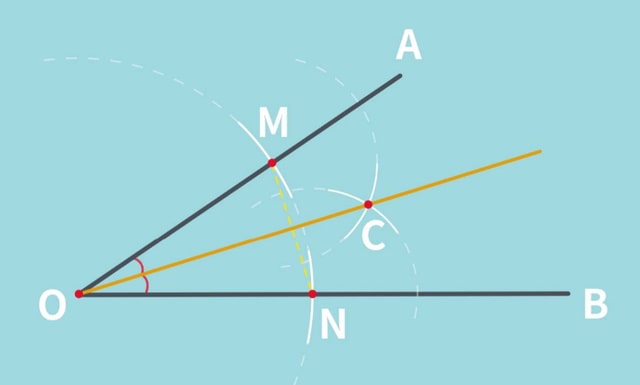
1、角平分線的性質(zhì)主要有角的平分線上的點到角的兩邊的距離相等，是指點到直線的距離，在應(yīng)用時必須含有垂直這個條件 否則不能得到線段相等，外角平分線上的點到角兩邊的反向延長線的距離相等，角的平分線上的點到角的兩邊的距離相等。

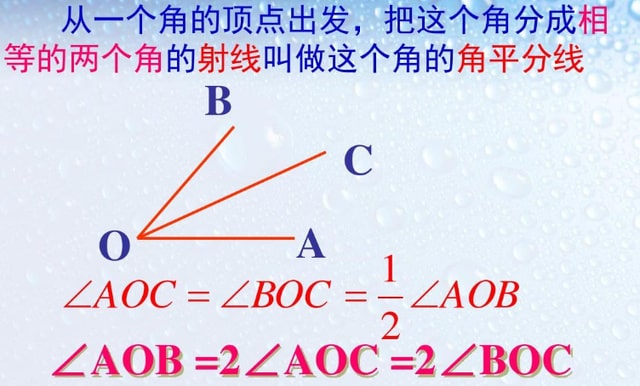
2、三角形內(nèi)角平分線的性質(zhì)定理是三角形的內(nèi)角平分線內(nèi)分對變成兩條線段，那么這兩條線段與這個角的兩邊對應(yīng)成比例，三角形內(nèi)角平分線的判定定理是在⊿ABC中，若點D按照邊AB和邊AC的比內(nèi)分邊BC,則線段AD是∠BAC的平分線。

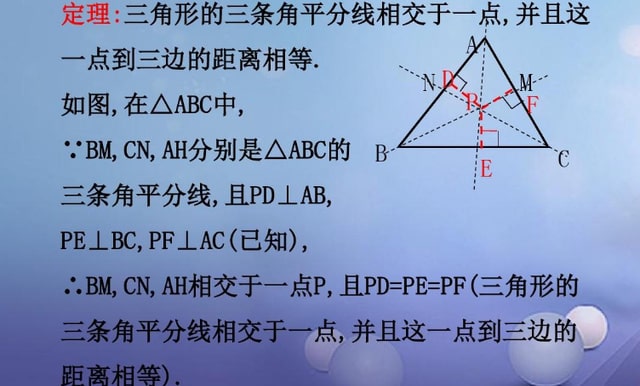
3、三角形的一個角的平分線與這個角的對邊相交，連接這個角的頂點和與對邊交點的線段叫作三角形的角平分線也叫三角形的內(nèi)角平分線，由定義可知三角形的角平分線是一條線段，由于三角形有三個內(nèi)角所以三角形有三條角平分線，三角形的角平分線交點一定在三角形內(nèi)部。